http://www.youtube.com/watch?v=iyEjD6Ri4iM&feature=related
Assinado:Lucas Dias
segunda-feira, 21 de novembro de 2011
quarta-feira, 16 de novembro de 2011
Representação na reta
Representação na reta |
| Os números inteiros relativos podem ser representados numa recta orientada. À direita de 0 marcamos os números positivos e à esquerda os números negativos. |
 |
| Como podemos observar, na recta orientada, ao ponto A corresponde o número +3. Desta forma dizemos que o ponto A tem abcissa +3. Também é possível representar qualquer número racional relativo numa recta orientada. A título de exemplo, iremos representar os números  , ,  e e que correspondem ao pontos G, H e I, respectivamente. que correspondem ao pontos G, H e I, respectivamente.O ponto G tem abcissa  , logo, teremos que dividir a primeira unidade positiva em três partes iguais, contar uma parte e marcar o ponto G. , logo, teremos que dividir a primeira unidade positiva em três partes iguais, contar uma parte e marcar o ponto G.O ponto H tem abcissa  e como a primeira unidade positiva só tem 3 partes, teremos que dividir as seguintes unidades até obter um número total de partes maior do que o numerador da fracção. De seguida conta-se 7 partes e marca-se o ponto H. e como a primeira unidade positiva só tem 3 partes, teremos que dividir as seguintes unidades até obter um número total de partes maior do que o numerador da fracção. De seguida conta-se 7 partes e marca-se o ponto H.O ponto I tem abcissa  , logo, teremos que dividir em três partes iguais a primeira unidade negativa, porque o ponto tem abcissa negativa. Mas, como o numerador é -4 teremos também que dividir a segunda unidade negativa, conta-se 4 partes e marca-se o ponto I. , logo, teremos que dividir em três partes iguais a primeira unidade negativa, porque o ponto tem abcissa negativa. Mas, como o numerador é -4 teremos também que dividir a segunda unidade negativa, conta-se 4 partes e marca-se o ponto I.Deste modo obtemos a seguinte representação: |
 |
Exercício 21 | |||||||
| Representa, numa recta orientada os seguintes números. | |||||||
|
| ||||||
Exercício 22 | ||
| Escreve as abcissas dos pontos indicados. | ||
 | ||
Ordenação |
| Dados dois números racionais é sempre possível saber qual é o maior. Na representação dos números na recta orientada o maior está sempre colocado à direita. |
 |
Exercício 23 | |||||||||||||
| Coloca os sinais de >, = ou <, de modo a obteres afirmações verdadeiras. | |||||||||||||
|
| ||||||||||||
Exercício 24 | |||||||
| As seguintes afirmações são verdadeiras ou falsas? Corrige as falsas. | |||||||
| |||||||
Postado por:Emily Eduarda .
Números inteiros
Os números naturais nasceram da nossa natural necessidade de contar elementos de um conjunto. Na adição de dois números naturais temos a propriedade do fechamento, que nos ensina que ao adicionarmos números naturais, o resultado-soma será sempre um número natural. No entanto, essa mesma propriedade do fechamento não é válida para a subtração de números naturais. Por isso não nos é possível a subtração de um número natural menor por um número natural maior que ele. No conjunto dos números naturais as subtrações abaixo não seriam possíveis.
Números inteiros 
Porém, há ocasiões em que precisamos apresentar um resultado para elas. Vejamos um exemplo Numa noite fria de inverno, a temperatura em Curitiba era de 7 graus centígrados e em Gramado, no Rio Grande do Sul era de apenas 1 grau centígrado. Se durante a madrugada fizesse ainda mais frio e a temperatura baixasse mais 4 graus, a quantos graus chegaria em Curitiba? E em Gramado? Como em Curitiba a temperatura era de 7 graus, baixando 4 graus ela chegaria a (7 - 4 ) graus, isto é, a 3 graus. Em Gramado, a temperatura era de 1 grau. Baixando 4 graus, ela chegaria a (1 - 4 ) graus. Para chegar a essa resposta, a matemática cria uma ampliação para o conjunto dos números naturais, ele inclui nele os números negativos, e dessa forma, a temperatura em Gramado seria de - 3 graus centígrados. De um modo geral, quantidades menores que zero, nós denominamos números negativos.
E quantidades maiores que o zero, nós denominamos números positivos.
Observamos que ao determinarmos números positivos e negativos, o número zero ocupa uma posição especial: ele é um número neutro, não é considerado positivo e nem negativo. À união dos números negativos, positivos e o zero faz surgir o conjunto dos números inteiros e é representado pela letra. Assim temos:

Vamos conhecer alguns subconjuntos importantes do conjunto dos números inteiros.

| Representação gráfica do conjunto dos números inteiros. |

| Números Inteiros Opostos ou Números Inteiros Simétricos. |
| Valor Absoluto ou Módulo de um Número Inteiro. |
Por :
Laís Júlia Brito Silva'. Origem dos Números Negativos
O número é um conceito fundamental em Matemática que tomou forma num longo desenvolvimento histórico. A origem e formulação deste conceito ocorreu simultaneamente com o despontar, entenda-se nascimento, e desenvolvimento da Matemática. As atividades práticas do homem, por um lado, e as exigências internas da Matemática por outro determinaram o desenvolvimento do conceito de número. A necessidade de contar objetos levou ao aparecimento do conceito de número Natural.
Todas as nações que desenvolveram formas de escrita introduziram o conceito de número Natural e desenvolveram um sistema de contagem. O desenvolvimento subsequente do conceito de número prosseguiu principalmente devido ao próprio desenvolvimento da Matemática. Os números negativos aparecem pela primeira vez na China antiga. Os chineses estavam acostumados a calcular com duas coleções de barras - vermelha para os números positivos e preta para os números negativos.No entanto, não aceitavam a ideia de um número negativo poder ser solução de uma equação. Os Matemáticos indianos descobriram os números negativos quando tentavam formular um algoritmo para a resolução de equações quadráticas. São exemplo disso as contribuições de Brahomagupta, pois a aritmética sistematizada dos números negativos encontra-se pela primeira vez na sua obra. As regras sobre grandezas eram já conhecidas através dos teoremas gregos sobre subtracção, como por exemplo (a -b)(c -d) = ac +bd -ad -bc, mas os hindus converteram-nas em regras numéricas sobre números negativos e positivos.
Diofanto (Séc. III) operou facilmente com os números negativos. Eles apareciam constantemente em cálculos intermédios em muitos problemas do seu "Aritmetika", no entanto havia certos problemas para o qual as soluções eram valores inteiros negativos como por exemplo:
4 = 4x +203x -18 = 5x^2
Nestas situações Diofanto limitava-se a classificar o problema de absurdo. Nos séculos XVI e XVII, muitos matemáticos europeus não apreciavam os números negativos e, se esses números apareciam nos seus cálculos, eles consideravam-nos falsos ou impossíveis. Exemplo deste facto seria Michael Stifel (1487- 1567) que se recusou a admitir números negativos como raízes de uma equação, chamando-lhes de "numeri absurdi". Cardano usou os números negativos embora chamando-os de "numeri ficti". A situação mudou a partir do (Séc.XVIII) quando foi descoberta uma interpretação geométrica dos números positivos e negativos como sendo segmentos de direções opostas.
Demonstração da regra dos sinais (segundo Euler)
Euler, um virtuoso do cálculo como se constata nos seus artigos científicos pela maneira audaz como manejava os números relativos e sem levantar questões quanto à legitimidade das suas construções forneceu uma explicação ou justificação para a regra os sinais. Consideremos os seus argumentos:
1- A multiplicação de uma dívida por um número positivo não oferece dificuldade, pois 3 dívidas de a escudos é uma dívida de 3a escudos, logo (b).(-a) = -ab.
2- Por comutatividade, Euler deduziu que (-a).(b) = -ab Destes dois argumentos conclui que o produto de uma quantidade positiva por uma quantidade negativa e vice-versa é uma quantidade negativa.
3- Resta determinar qual o produto de (-a) por (-b). É evidente diz Euler que o valor absoluto é ab. É pois então necessário decidir-se entre ab ou -ab. Mas como (-a) ´ b é -ab, só resta como única possibilidade que (-a).(-b) = +ab.
É claro que este tipo de argumentação vem demonstrar que qualquer "espírito" mais zeloso, como Stendhal, não pode ficar satisfeito, pois principalmente o terceiro argumento de Euler não consegue provar ou mesmo justificar coerentemente que - por - = +. No fundo, este tipo de argumentação denota que Euler não tinha ainda conhecimentos suficientes para justificar estes resultados aceitalvelmente. Na mesma obra de Euler podemos verificar que ele entende os números negativos como sendo apenas uma quantidade que se pode representar por uma letra precedida do sinal - (menos). Euler não compreende ainda que os números negativos são quantidades menores que zero.
Todas as nações que desenvolveram formas de escrita introduziram o conceito de número Natural e desenvolveram um sistema de contagem. O desenvolvimento subsequente do conceito de número prosseguiu principalmente devido ao próprio desenvolvimento da Matemática. Os números negativos aparecem pela primeira vez na China antiga. Os chineses estavam acostumados a calcular com duas coleções de barras - vermelha para os números positivos e preta para os números negativos.No entanto, não aceitavam a ideia de um número negativo poder ser solução de uma equação. Os Matemáticos indianos descobriram os números negativos quando tentavam formular um algoritmo para a resolução de equações quadráticas. São exemplo disso as contribuições de Brahomagupta, pois a aritmética sistematizada dos números negativos encontra-se pela primeira vez na sua obra. As regras sobre grandezas eram já conhecidas através dos teoremas gregos sobre subtracção, como por exemplo (a -b)(c -d) = ac +bd -ad -bc, mas os hindus converteram-nas em regras numéricas sobre números negativos e positivos.
Diofanto (Séc. III) operou facilmente com os números negativos. Eles apareciam constantemente em cálculos intermédios em muitos problemas do seu "Aritmetika", no entanto havia certos problemas para o qual as soluções eram valores inteiros negativos como por exemplo:
4 = 4x +203x -18 = 5x^2
Nestas situações Diofanto limitava-se a classificar o problema de absurdo. Nos séculos XVI e XVII, muitos matemáticos europeus não apreciavam os números negativos e, se esses números apareciam nos seus cálculos, eles consideravam-nos falsos ou impossíveis. Exemplo deste facto seria Michael Stifel (1487- 1567) que se recusou a admitir números negativos como raízes de uma equação, chamando-lhes de "numeri absurdi". Cardano usou os números negativos embora chamando-os de "numeri ficti". A situação mudou a partir do (Séc.XVIII) quando foi descoberta uma interpretação geométrica dos números positivos e negativos como sendo segmentos de direções opostas.
Demonstração da regra dos sinais (segundo Euler)
Euler, um virtuoso do cálculo como se constata nos seus artigos científicos pela maneira audaz como manejava os números relativos e sem levantar questões quanto à legitimidade das suas construções forneceu uma explicação ou justificação para a regra os sinais. Consideremos os seus argumentos:
1- A multiplicação de uma dívida por um número positivo não oferece dificuldade, pois 3 dívidas de a escudos é uma dívida de 3a escudos, logo (b).(-a) = -ab.
2- Por comutatividade, Euler deduziu que (-a).(b) = -ab Destes dois argumentos conclui que o produto de uma quantidade positiva por uma quantidade negativa e vice-versa é uma quantidade negativa.
3- Resta determinar qual o produto de (-a) por (-b). É evidente diz Euler que o valor absoluto é ab. É pois então necessário decidir-se entre ab ou -ab. Mas como (-a) ´ b é -ab, só resta como única possibilidade que (-a).(-b) = +ab.
É claro que este tipo de argumentação vem demonstrar que qualquer "espírito" mais zeloso, como Stendhal, não pode ficar satisfeito, pois principalmente o terceiro argumento de Euler não consegue provar ou mesmo justificar coerentemente que - por - = +. No fundo, este tipo de argumentação denota que Euler não tinha ainda conhecimentos suficientes para justificar estes resultados aceitalvelmente. Na mesma obra de Euler podemos verificar que ele entende os números negativos como sendo apenas uma quantidade que se pode representar por uma letra precedida do sinal - (menos). Euler não compreende ainda que os números negativos são quantidades menores que zero.
RAFAELA PEREIRA
Número negativo
Em matemática, define-se como número negativo todo número real menor que zero, como o −1 e o −3. Dois números são chamados de números simétricos quando estão à mesma distância do zero, como o −5 e o 5.Na Física o termo também serve para dar nome às cargas existentes em partículas eletricamente carregadas. A atribuição de carga negativa ao electrão e positiva ao protão é totalmente arbitrária, e tem razões históricas.
RAFAELA PEREIRA
HISTÓRIA DOS NUMEROS NEGATIVOS
Durante séculos, foram considerados absurdos e inconcebíveis. Os números serviam para contar ou para exprimir medidas, e não há rebanhos com número negativo de carneiros, nem campos com número negativo de comprimento… Enquanto a noção de número estiver ligada a noções de grandeza ou de quantidade, os números negativos não podiam ser, naturalmente, concebidos nem aceites.
Mas eles teimavam em aparecer nas soluções dos problemas. E os matemáticos davam cabo da cabeça para encontrar métodos para resolver esses problemas sem usar os disparatados números negativos. Por exemplo, se se procurava o valor de um número x que, somado a 100, desse 50, e se encontrava -50, isso queria dizer que era o problema que estava mal formulado, e que em vez de somar, se deveria ter subtraído… Como não havia “quantidades negativas”, a subtracção de “quantidades positivas” era o expediente mais utilizado para conseguir “ignorar” os números negativos. Curiosamente, isto fez com que as regras de cálculo dos números negativos se tivessem desenvolvido antes de eles serem aceites na selecta sociedade dos sábios.
Hoje, os números negativos fazem parte do nosso quotidiano. Basta ligar a TV e ouvir os Boletins Metereológicos de Inverno para sabermos que, no Norte da Europa, ou na Sibéria, as temperaturas foram de -5, -10 ou -50 graus (negativos, isto é, abaixo de zero)… Sem que isso nos faça confusão.
vanesssa
quinta-feira, 10 de novembro de 2011
Regras da
matemática
As regras são as seguintes: na multiplicação e divisão, sinais iguais dá positivo, sinais diferentes dá negativo. Na subtração e adição, sinais iguais somam e conservam o sinal, sinais diferentes subtraem e dá o sinal do maior número.
1.Adicionando regras:
Positivo + positivo = positivo: 5
+ 4 = 9
Negativo + negativo = negativo: (- 7) + (- 2) = - 9
Negativo + negativo = negativo: (- 7) + (- 2) = - 9
Soma de um negativo e um número
positivo: Use o sinal do maior número e subtrair
(- 7) + 4 = -3
6 + (-9) = - 3
(- 3) + 7 = 4
5 + (-3) = 2
6 + (-9) = - 3
(- 3) + 7 = 4
5 + (-3) = 2
2.Subtraindo
Regras:
Negativo - positivo = negativo: (-
5) - 3 = -5 + (-3) = -8
Positivo - Negativo = positivo + positivo = positivo: 5 - (-3) = 5 + 3 = 8
Negativas - Negativo = Negativo + Positivo = Use o sinal do maior número e subtrair (Alterar duplas negativas para um positivo)
(-5) - (-3) = (-5) + 3 = -2
(-3) - (-5) = (-3) + 5 = 2
Positivo - Negativo = positivo + positivo = positivo: 5 - (-3) = 5 + 3 = 8
Negativas - Negativo = Negativo + Positivo = Use o sinal do maior número e subtrair (Alterar duplas negativas para um positivo)
(-5) - (-3) = (-5) + 3 = -2
(-3) - (-5) = (-3) + 5 = 2
3.Multiplicando
Regras:
Positiva x = Positivo Positivo: 3
x 2 = 6
Negativo x = Negativo Positivo: (-2) x (-8) = 16
Negativo x positivo = negativo: (-3) x 4 = -12
Positivo x Negativo = Negativo: 3 x (-4) = -12
Negativo x = Negativo Positivo: (-2) x (-8) = 16
Negativo x positivo = negativo: (-3) x 4 = -12
Positivo x Negativo = Negativo: 3 x (-4) = -12
4.Dividindo
Regras:
Positiva ÷ positivo = positivo: 12
÷ 3 = 4
Negativos ÷ Negativo = Positivo: = (-12) ÷ (-3) 4
Negativos ÷ positivo = negativo: (-12) ÷ 3 = -4
Positiva ÷ Negativo = Negativo: 12 ÷ (-3) = -4
Negativos ÷ Negativo = Positivo: = (-12) ÷ (-3) 4
Negativos ÷ positivo = negativo: (-12) ÷ 3 = -4
Positiva ÷ Negativo = Negativo: 12 ÷ (-3) = -4
Aluna:Luana Oliveira Andrade
Número negativos
Número negativo
Em matemática, define-se como número negativo todo número real menor que zero, como o −1 e o −3. Dois números são chamados de números simétricos quando estão à mesma distância do zero, como o−5 e o 5.
Regras da matemática
As regras são as seguintes: na multiplicação e divisão, sinais iguais dá positivo, sinais diferentes dá negativo. Na subtração e adição, sinais iguais somam e conservam o sinal, sinais diferentes subtraem e dá o sinal do maior número.
Aluna:Luana Oliveira Andrade
quarta-feira, 9 de novembro de 2011
ORIGEM DOS NÚMEROS NEGATIVOS
O número é um conceito fundamental em Matemática que tomou forma num longo desenvolvimento histórico. A origem e formulação deste conceito ocorreu simultaneamente com o despontar, entenda-se nascimento, e desenvolvimento da Matemática. As atividades práticas do homem, por um lado, e as exigências internas da Matemática por outro determinaram o desenvolvimento do conceito de número. A necessidade de contar objetos levou ao aparecimento do conceito de número Natural.
Todas as nações que desenvolveram formas de escrita introduziram o conceito de número Natural e desenvolveram um sistema de contagem. O desenvolvimento subsequente do conceito de número prosseguiu principalmente devido ao próprio desenvolvimento da Matemática. Os números negativos aparecem pela primeira vez na China antiga. Os chineses estavam acostumados a calcular com duas coleções de barras - vermelha para os números positivos e preta para os números negativos.No entanto, não aceitavam a ideia de um número negativo poder ser solução de uma equação. Os Matemáticos indianos descobriram os números negativos quando tentavam formular um algoritmo para a resolução de equações quadráticas. São exemplo disso as contribuições de Brahomagupta, pois a aritmética sistematizada dos números negativos encontra-se pela primeira vez na sua obra. As regras sobre grandezas eram já conhecidas através dos teoremas gregos sobre subtracção, como por exemplo (a -b)(c -d) = ac +bd -ad -bc, mas os hindus converteram-nas em regras numéricas
sobre números negativos e positivos.
sobre números negativos e positivos.
Diofanto (Séc. III) operou facilmente com os números negativos. Eles apareciam constantemente em cálculos intermédios em muitos problemas do seu "Aritmetika", no entanto havia certos problemas para o qual as soluções eram valores inteiros negativos como por exemplo:
4 = 4x +20
3x -18 = 5x^2
3x -18 = 5x^2
Nestas situações Diofanto limitava-se a classificar o problema de absurdo. Nos séculos XVI e XVII, muitos matemáticos europeus não apreciavam os números negativos e, se esses números apareciam nos seus cálculos, eles consideravam-nos falsos ou impossíveis. Exemplo deste facto seria Michael Stifel (1487- 1567) que se recusou a admitir números negativos como raízes de uma equação, chamando-lhes de "numeri absurdi". Cardano usou os números negativos embora chamando-os de "numeri ficti". A situação mudou a partir do (Séc.XVIII) quando foi descoberta uma interpretação geométrica dos números positivos e negativos como sendo segmentos de direções opostas.
Demonstração da regra dos sinais (segundo Euler)
Euler, um virtuoso do cálculo como se constata nos seus artigos científicos pela maneira audaz como manejava os números relativos e sem levantar questões quanto à legitimidade das suas construções forneceu uma explicação ou justificação para a regra os sinais. Consideremos os seus argumentos:
1- A multiplicação de uma dívida por um número positivo não oferece dificuldade, pois 3 dívidas de a escudos é uma dívida de 3a escudos, logo (b).(-a) = -ab.
2- Por comutatividade, Euler deduziu que (-a).(b) = -ab
Destes dois argumentos conclui que o produto de uma quantidade positiva por uma quantidade negativa e vice-versa é uma quantidade negativa.
Destes dois argumentos conclui que o produto de uma quantidade positiva por uma quantidade negativa e vice-versa é uma quantidade negativa.
3- Resta determinar qual o produto de (-a) por (-b). É evidente diz Euler que o valor absoluto é ab. É pois então necessário decidir-se entre ab ou -ab. Mas como (-a) ´ b é -ab, só resta como única possibilidade que (-a).(-b) = +ab.
É claro que este tipo de argumentação vem demonstrar que qualquer "espírito" mais zeloso, como Stendhal, não pode ficar satisfeito, pois principalmente o terceiro argumento de Euler não consegue provar ou mesmo justificar coerentemente que - por - = +. No fundo, este tipo de argumentação denota que Euler não tinha ainda conhecimentos suficientes para justificar estes resultados aceitalvelmente. Na mesma obra de Euler podemos verificar que ele entende os números negativos como sendo apenas uma quantidade que se pode representar por uma letra precedida do sinal - (menos). Euler não compreende ainda que os números negativos são quantidades menores que zero.
domingo, 6 de novembro de 2011
Peso X Massa .
.jpg)
O peso é calculado de acordo com a
aceleração local da gravidade
aceleração local da gravidade
É comum ouvirmos as seguintes frases: “Eu peso 85 kg”, “Estou acima do meu peso”, “O peso ideal para sua altura é 75 kg”. Popularmente, estamos associando a medida observada ao subirmos em uma balança à palavra peso. Essa argumentação utilizada por grande parte das pessoas está totalmente equivocada, pois não podemos relacionar peso com a massa de um corpo, que é a grandeza verificada na balança. As definições corretas são:
Peso é uma força “invisível” que atrai os corpos para a superfície da terra. Dessa forma, o nosso peso varia de acordo com o valor da gravidade, diferente em outros planetas e satélites naturais do sistema solar.
Massa é a quantidade de matéria presente em um corpo. Dizemos que a massa de uma pessoa é a mesma em qualquer lugar.
Por exemplo, vamos imaginar que uma pessoa tenha massa de 60 kg. De acordo com essa medida, podemos dizer que ela possui peso igual a aproximadamente 588 N (Newton). Vamos entender o valor desse peso:
Quando nos referimos ao peso, dizendo que seu valor depende da gravidade, então estamos colocando em prática a 2ª lei de Newton, demonstrada pela fórmula matemática: P = m * g. Nessa expressão, temos que:
P: peso
m: massa
g: aceleração da gravidade
Continuando com mais um exemplo, vamos determinar o peso de uma pessoa com massa igual a 57 kg, na terra, na lua e em outros planetas. Mas para isso, precisamos conhecer as acelerações da gravidade que estão presentes na tabela a seguir:
.jpg)
Uma pessoa com a massa igual a 57 kg possui os seguintes pesos:
Na terra
P = m * g → P = 57 * 9,8 → P = 558,6 N
Na lua
P = m * g → P = 57 * 1,67 → P = 95,19 N
Em Júpiter
P = 57 * 22,9 → P = 1 305,3 N
Em Plutão
P = 57 * 0,5 → P = 28,5 N
No sol
P = 57 * 274 → P = 15 618 N
Na terra
P = m * g → P = 57 * 9,8 → P = 558,6 N
Na lua
P = m * g → P = 57 * 1,67 → P = 95,19 N
Em Júpiter
P = 57 * 22,9 → P = 1 305,3 N
Em Plutão
P = 57 * 0,5 → P = 28,5 N
No sol
P = 57 * 274 → P = 15 618 N
Por Laís Júlia Brito Silva .
Razão
Dizemos que a razão entre dois números a e b é a relação a/b, onde a e b são números reais com b ≠ 0. Dessa forma, concluímos que razão é uma fração, a qual é utilizada no intuito de comparar grandezas. A razão pode ser representada por uma fração, um número na forma decimal, porcentagem ou até mesmo por uma divisão. Por exemplo:
3 : 5 = 3/5 = 0,6 = 60%
1 : 10 = 1/10 = 0,1 = 10%
Para entendermos a ideia principal de uma razão, observe os exemplos a seguir:
Exemplo 1
Em uma turma de preparatório para o vestibular, o número de mulheres é igual a 50 e o número de homens é 40. Determine:
a) a razão entre o número de homens e o número de mulheres.
Temos 40 homens para 50 mulheres, então: 40/50 que simplificado fica 4/5. Concluímos que para cada cinco mulheres existem quatro homens.
b) a razão entre o número de homens e de mulheres na forma de porcentagem.
40/50 = 0,8 = 80%
Exemplo 2
Em uma prova de testes, Carlos acertou 28 questões e errou 12. Escreva na forma de fração:
a) a razão entre o número de acertos e o número de erros.
28/12, simplificando fica 7/3
b) a razão entre o número de erros e o número de acertos.
12/28 simplificando temos 3/7
c) a razão entre o número de acertos e o número total de questões.
28/40 simplificando temos 7/10
Exemplo 3
Em um jogo de basquete, a equipe de Pedro e de José marcou 60 pontos, dos quais Pedro marcou 20 pontos e José marcou 15. Com base nessas informações determine:
a) a razão entre o número de pontos marcados por José e o número de pontos marcados por Pedro.
15/20 simplificando temos 3/4
b) razão entre o número de pontos marcados por Pedro e o número de pontos marcados pela equipe.
20/60 que simplificado fica 1/3
Na resolução dos exemplos você pôde notar que a ordem dos números no cálculo de uma razão é muito importante. Dessa forma, cada um recebe um nome. O numerador é denominado antecedente e o denominador recebe o nome de consequente.
3 : 5 = 3/5 = 0,6 = 60%
1 : 10 = 1/10 = 0,1 = 10%
Para entendermos a ideia principal de uma razão, observe os exemplos a seguir:
Exemplo 1
Em uma turma de preparatório para o vestibular, o número de mulheres é igual a 50 e o número de homens é 40. Determine:
a) a razão entre o número de homens e o número de mulheres.
Temos 40 homens para 50 mulheres, então: 40/50 que simplificado fica 4/5. Concluímos que para cada cinco mulheres existem quatro homens.
b) a razão entre o número de homens e de mulheres na forma de porcentagem.
40/50 = 0,8 = 80%
Exemplo 2
Em uma prova de testes, Carlos acertou 28 questões e errou 12. Escreva na forma de fração:
a) a razão entre o número de acertos e o número de erros.
28/12, simplificando fica 7/3
b) a razão entre o número de erros e o número de acertos.
12/28 simplificando temos 3/7
c) a razão entre o número de acertos e o número total de questões.
28/40 simplificando temos 7/10
Exemplo 3
Em um jogo de basquete, a equipe de Pedro e de José marcou 60 pontos, dos quais Pedro marcou 20 pontos e José marcou 15. Com base nessas informações determine:
a) a razão entre o número de pontos marcados por José e o número de pontos marcados por Pedro.
15/20 simplificando temos 3/4
b) razão entre o número de pontos marcados por Pedro e o número de pontos marcados pela equipe.
20/60 que simplificado fica 1/3
Na resolução dos exemplos você pôde notar que a ordem dos números no cálculo de uma razão é muito importante. Dessa forma, cada um recebe um nome. O numerador é denominado antecedente e o denominador recebe o nome de consequente.
Por Laís Júlia Brito Silva
sábado, 5 de novembro de 2011
sexta-feira, 4 de novembro de 2011
PARABÉNS!!!
Parabenizo meus queridos alunos do 7º Ano do Ensino Fundamental da Escola Municipal Professora "Umbelina Azevedo Avellar" pelo comprometimento, seriedade e vontade em adquirir uma aprendizagem significativa em Matemática.
Abraços da professora: Fabiana Perla Barcelos
A matemática na escola
A matemática que se estuda na escola aplica-se facilmente às necessidades quotidianas. Isto é obvio até ao 9º ano mas no ensino secundário parece que ela não tem tanta utilidade. Mas não é por acaso que se estuda matemática nas escolas.
 Antes de mais, ela é útil para promover o pensamento estruturado e o raciocínio rigoroso. Por outro lado, a sociedade evoluiu exigindo cada vez mais conhecimentos matemáticos a todos os cidadão. Um arquitecto dirá que a Matemática é útil para auxiliar a percepção e a criação da beleza; um engenheiro dirá que é útil para reforçar e aprovar experiências; um físico dirá que é útil por ser a linguagem da ciência; um político dirá que a Matemática orienta-o na administração e na implementação de leis; um psicólogo afirmará que auxilia-o no tratamento estatístico de inquéritos; um matemático mostrará que um corpo matemático é útil quando for aplicável a outro corpo. A matemática é um saber necessário a todas as disciplinas e ciências, devido ao seu rigor. Deste modo se mostra que as outras ciências não se desenvolveriam se a matemática não existisse e não fosse estudada. De certa forma todos somos matemáticos e fazemos matemática com regularidade: fazer as contas das compras; medir uma divisão para pôr alcatifa; escolher itinerários; relacionar conjuntos de bens; inferir e concluir a partir de premissas; etc. E confiamos sempre na exactidão dos nossos raciocínios até prova em contrário.
Antes de mais, ela é útil para promover o pensamento estruturado e o raciocínio rigoroso. Por outro lado, a sociedade evoluiu exigindo cada vez mais conhecimentos matemáticos a todos os cidadão. Um arquitecto dirá que a Matemática é útil para auxiliar a percepção e a criação da beleza; um engenheiro dirá que é útil para reforçar e aprovar experiências; um físico dirá que é útil por ser a linguagem da ciência; um político dirá que a Matemática orienta-o na administração e na implementação de leis; um psicólogo afirmará que auxilia-o no tratamento estatístico de inquéritos; um matemático mostrará que um corpo matemático é útil quando for aplicável a outro corpo. A matemática é um saber necessário a todas as disciplinas e ciências, devido ao seu rigor. Deste modo se mostra que as outras ciências não se desenvolveriam se a matemática não existisse e não fosse estudada. De certa forma todos somos matemáticos e fazemos matemática com regularidade: fazer as contas das compras; medir uma divisão para pôr alcatifa; escolher itinerários; relacionar conjuntos de bens; inferir e concluir a partir de premissas; etc. E confiamos sempre na exactidão dos nossos raciocínios até prova em contrário.
Podemos considerar que a aprendizagem da matemática nas escolas é paralela ao desenvolvimento da humanidade. O Homem há 10 mil anos mal sabia contar e agora calcula a trajectória de um satélite. De modo semelhante, uma criança aprende a contar com 6 anos e ao longo da sua adolescência vai aprendendo em pouco tempo aquilo que levou anos e anos a ser inventado. A matemática conhecida por um aluno do 9º ano impressionaria o rei D. Afonso V e certamente o convidaria para trabalhar na corte.
assinado: rafaela pereira
 Antes de mais, ela é útil para promover o pensamento estruturado e o raciocínio rigoroso. Por outro lado, a sociedade evoluiu exigindo cada vez mais conhecimentos matemáticos a todos os cidadão. Um arquitecto dirá que a Matemática é útil para auxiliar a percepção e a criação da beleza; um engenheiro dirá que é útil para reforçar e aprovar experiências; um físico dirá que é útil por ser a linguagem da ciência; um político dirá que a Matemática orienta-o na administração e na implementação de leis; um psicólogo afirmará que auxilia-o no tratamento estatístico de inquéritos; um matemático mostrará que um corpo matemático é útil quando for aplicável a outro corpo. A matemática é um saber necessário a todas as disciplinas e ciências, devido ao seu rigor. Deste modo se mostra que as outras ciências não se desenvolveriam se a matemática não existisse e não fosse estudada.
Antes de mais, ela é útil para promover o pensamento estruturado e o raciocínio rigoroso. Por outro lado, a sociedade evoluiu exigindo cada vez mais conhecimentos matemáticos a todos os cidadão. Um arquitecto dirá que a Matemática é útil para auxiliar a percepção e a criação da beleza; um engenheiro dirá que é útil para reforçar e aprovar experiências; um físico dirá que é útil por ser a linguagem da ciência; um político dirá que a Matemática orienta-o na administração e na implementação de leis; um psicólogo afirmará que auxilia-o no tratamento estatístico de inquéritos; um matemático mostrará que um corpo matemático é útil quando for aplicável a outro corpo. A matemática é um saber necessário a todas as disciplinas e ciências, devido ao seu rigor. Deste modo se mostra que as outras ciências não se desenvolveriam se a matemática não existisse e não fosse estudada.Podemos considerar que a aprendizagem da matemática nas escolas é paralela ao desenvolvimento da humanidade. O Homem há 10 mil anos mal sabia contar e agora calcula a trajectória de um satélite. De modo semelhante, uma criança aprende a contar com 6 anos e ao longo da sua adolescência vai aprendendo em pouco tempo aquilo que levou anos e anos a ser inventado. A matemática conhecida por um aluno do 9º ano impressionaria o rei D. Afonso V e certamente o convidaria para trabalhar na corte.
assinado: rafaela pereira
Onde podemos encontrar a matemática?
Nos livros, filmes, desenhos, computadores e um pouco por toda a natureza.
Poderemos ver um "segmento de recta" na aresta de um edifício, uma circunferência vê-se na ondulação da superfície da água quando deixamos cair um objecto, uma secção da elipse pode ser observada na parede de um poço redondo iluminado pelo sol, as sombras dos objectos representam figuras geométricas, na disposição das pétalas de uma flor podem encontrar-se simetrias, o batimento cardíaco pode ser um exemplo de uma sucessão, o ar move-se num percurso espiralado, etc. "O estudo aprofundado da natureza é a fonte mais fecunda das descobertas matemáticas" (Joseph Fourrier). Assim, até parece que "o universo impôs a matemática à humanidade" ([ 1] p76).
"Aquela por vezes cristalina [ ...] e por vezes difusa substância [ ...] que é a matemática" (Imre Lakatos), trata de figuras, sólidos e suas propriedades na Geometria; sintetiza problemas do comércio, seguros e finanças através da Álgebra e da Análise; estuda e estrutura dados com a Estatística; desenvolve a Química e a Física com a Análise; estuda os percursos rodoviários e aéreos com a Teoria de grafos; apoia a estrutura das línguas com a Lógica. A esta matemática que é utilizada fora de si mesma chama-se matemática aplicada. E milhares de outras subcategorias da matemática podem aplicar-se a diversos outros saberes (Ap. C). Até a investigação criminal poderia bem ser considerada um ramo da matemática, como chegou a afirmar Conan Doyle.
Mas muita matemática que se faz actualmente não é imediatamente aplicável, podendo vir a ser um forte contributo para as teorias de outros saberes ou a ficar para sempre esquecida.

A matemática é cada vez menos fruto do trabalho isolado de uma pessoa. Mas antes resulta de um grupo de matemáticos ou das relações profissionais entre várias pessoas. Ou ainda, é um esforço que pode demorar séculos.
Ao longo da história muitos homens contribuíram significativamente para o seu desenvolvimento (Ap. B). O trabalho de um foi analisado por outro matemático e assim sucessivamente até ao presente, sendo muitas vezes melhorado.
Nem sempre o que um matemático faz está correcto. Ele também se engana. Não é um ser superior nem vive em casulos. E quando um erro lhe é apontado, verifica, reconhece-o e agradece com delicadeza. Que ferramentas são necessárias para a investigação matemática? Muitos podem pensar que é suficiente um lápis e muita massa cinzenta. Mas a matemática não é feita apenas dentro da cabeça. Há muitos utensílios que auxiliam a sua produção: o compasso desenha circunferências; a régua traça segmentos de rectas;o esquadro desenha |  |
ângulos; o transferidor mede a amplitude de um ângulo; o pantógrafo desenha figuras semelhantes; a calculadora efectua cálculos; . . . ; o computador representa objectos impossíveis.
Uma ferramenta cada vez mais precioso é o computador. Com ele é agora possível fazer cálculos que um homem levaria anos a fazer.Com estes instrumentos, a matemática também pode construir realidades.
assinado: rafaela pereira
Como surgiu a matemática?
As origens da matemática perdem-se no tempo. Os mais antigos registos matemáticos de que se tem conhecimento datam de 2400 a.C. Progressivamente, o homem foi reflectindo acerca do que se sabia e do que se queria saber. Algumas tribos apenas conheciam o "um", "dois" e "muitos". Os seus problemas do quotidiano, como a contagem e a medida de comprimentos e de áreas, sugeriram a invenção de conceitos cada vez mais perfeitos. Os "Elementos" do grego Euclides (séc. IV a.C.) foram dos primeiros livros de matemática que apresentaram de forma sistemática a construção dos teoremas da geometria e foram utilizados no ensino em todo o mundo até ao século XVII. Mesmo a antiquíssima Astrologia proporcionou o desenvolvimento da matemática, ao exigir a construção de definições e o rigor no cálculo das posições dos astros.
A matemática começou por ser "a ciência que tem por objecto a medida e as propriedades das grandezas" (dicionário), mas actualmente é cada vez mais a ciência do padrão e da estrutura dedutiva. Como afirmou P. Dirac, as matemáticas são a ferramenta especialmente adaptada ao tratamento das noções abstractas de qualquer natureza e, neste domínio, seu poder é ilimitado.
A etnomatemática é um ramo recente da matemática que investiga conhecimentos matemáticos populares ([ 2] p.p. 27-47). E podemos afirmar que todos os povos têm alguns conhecimentos de matemática, mesmo que sejam muito intuitivos tais como medições, proporções, desenhos geométricos que se vêem no artesanato (como a cestaria).
A matemática sempre desempenhou um papel único no desenvolvimento das sociedades (Ap. A). Por exemplo, numa situação de guerra, o exército que possui mais conhecimentos de matemática tem maior poder traduzido nas máquinas mais perfeitas e melhor adaptadas.
Até ao séc. XVI apenas as pessoas com dinheiro ou os sacerdotes poderiam despender tempo no estudo da matemática. De há quatrocentos anos para cá, a monarquia e o clero deixaram de ser os únicos que financiaram a matemática, passando este papel a ser desempenhado pelas universidades e pelas empresas (como por exemplo a IBM). Ao contrário do que muitos pensam, amatemática não consiste apenas em demostrar teoremas ou em fazer contas, ela um autêntico tesouro para a civilização devido aos diversos conhecimentos envolvidos. E sabendo isso, actualmente poucos são os países em que não se cria matemática nova, publicando-se assim em todo o mundo alguns milhares de revistas exclusivamente de matemática.
assinado: rafaela pereira
Sokoban
Para jogar basta clicar no link a baixo:
http://www.somatematica.com.br/jogos/sokoban/sokoban.html
Postado por : Laís Brito
http://www.somatematica.com.br/jogos/sokoban/sokoban.html
Postado por : Laís Brito
Palavras Cruzadas .
Para jogar basta clicar no link abaixo :
http://www.somatematica.com.br/palavras/puzzle15494.html
Porstado por : Laís Brito .
http://www.somatematica.com.br/palavras/puzzle15494.html
Porstado por : Laís Brito .
Principais áreas da Matemática :
- Aritmética
- Álgebra
- Geometria
- Geometria Analítica
- Porcentagem
- Trigonometria
- Estatística
- Educação Matemática
- Álgebra
- Geometria
- Geometria Analítica
- Porcentagem
- Trigonometria
- Estatística
- Educação Matemática
Assinado aluna : Luana Andrade
Coisas de matemática
A beleza da Matemática
1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111
9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
Brilhante, não é?
E que tal esta simetria:
1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
Frações, divisibilidade, proporções e razoes
O símbolo 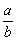 significa a:b, sendo a e b números naturais e b diferente de zero.
significa a:b, sendo a e b números naturais e b diferente de zero.
Chamamos:

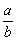 de fração;
de fração;
 a de numerador;
a de numerador;
 b de denominador.
b de denominador.
Se a é múltiplo de b, então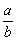 é um número natural.
é um número natural.
Veja um exemplo:
A fração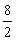 é igual a 8:2. Neste caso, 8 é o numerador e 2 é o denominador. Efetuando a divisão de 8 por 2, obtemos o quociente 4. Assim,
é igual a 8:2. Neste caso, 8 é o numerador e 2 é o denominador. Efetuando a divisão de 8 por 2, obtemos o quociente 4. Assim, 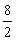 é um número natural e 8 é múltiplo de 2.
é um número natural e 8 é múltiplo de 2.
Durante muito tempo, os números naturais foram os únicos conhecidos e usados pelos homens. Depois começaram a surgir questões que não poderiam ser resolvidas com números naturais. Então surgiu o conceito de número fracionário.
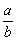 significa a:b, sendo a e b números naturais e b diferente de zero.
significa a:b, sendo a e b números naturais e b diferente de zero. Chamamos:

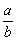 de fração;
de fração; a de numerador;
a de numerador; b de denominador.
b de denominador.Se a é múltiplo de b, então
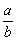 é um número natural.
é um número natural.Veja um exemplo:
A fração
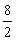 é igual a 8:2. Neste caso, 8 é o numerador e 2 é o denominador. Efetuando a divisão de 8 por 2, obtemos o quociente 4. Assim,
é igual a 8:2. Neste caso, 8 é o numerador e 2 é o denominador. Efetuando a divisão de 8 por 2, obtemos o quociente 4. Assim, 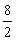 é um número natural e 8 é múltiplo de 2.
é um número natural e 8 é múltiplo de 2.Durante muito tempo, os números naturais foram os únicos conhecidos e usados pelos homens. Depois começaram a surgir questões que não poderiam ser resolvidas com números naturais. Então surgiu o conceito de número fracionário.
sexta-feira, 28 de outubro de 2011
ORIGEM DOS NÚMEROS NEGATIVOS
Todas as nações que desenvolveram formas de escrita introduziram o conceito de número Natural e desenvolveram um sistema de contagem. O desenvolvimento subsequente do conceito de número prosseguiu principalmente devido ao próprio desenvolvimento da Matemática. Os números negativos aparecem pela primeira vez na China antiga. Os chineses estavam acostumados a calcular com duas coleções de barras - vermelha para os números positivos e preta para os números negativos.No entanto, não aceitavam a ideia de um número negativo poder ser solução de uma equação. Os Matemáticos indianos descobriram os números negativos quando tentavam formular um algoritmo para a resolução de equações quadráticas. São exemplo disso as contribuições de Brahomagupta, pois a aritmética sistematizada dos números negativos encontra-se pela primeira vez na sua obra. As regras sobre grandezas eram já conhecidas através dos teoremas gregos sobre subtracção, como por exemplo (a -b)(c -d) = ac +bd -ad -bc, mas os hindus converteram-nas em regras numéricas sobre números negativos e positivos.
Diofanto (Séc. III) operou facilmente com os números negativos. Eles apareciam constantemente em cálculos intermédios em muitos problemas do seu "Aritmetika", no entanto havia certos problemas para o qual as soluções eram valores inteiros negativos como por exemplo:
4 = 4x +20
3x -18 = 5x^2
3x -18 = 5x^2
Nestas situações Diofanto limitava-se a classificar o problema de absurdo. Nos séculos XVI e XVII, muitos matemáticos europeus não apreciavam os números negativos e, se esses números apareciam nos seus cálculos, eles consideravam-nos falsos ou impossíveis. Exemplo deste facto seria Michael Stifel (1487- 1567) que se recusou a admitir números negativos como raízes de uma equação, chamando-lhes de "numeri absurdi". Cardano usou os números negativos embora chamando-os de "numeri ficti". A situação mudou a partir do (Séc.XVIII) quando foi descoberta uma interpretação geométrica dos números positivos e negativos como sendo segmentos de direções opostas.
NÚMEROS INTEIROS – NÚMEROS NEGATIVOS
Os inteiros, ou números inteiros, consistem dos números naturais (0, 1, 2, ...) e dos números inteiros negativos (-1, -2, -3, ...). O conjunto de todos os inteiros é normalmente chamado de Z (Mais apropriadamente, um Z em blackboard bold, Z), que vem de Zahlen (do alemão, "número").
Inteiros podem ser adicionados ou subtraídos, multiplicados e comparados. A principal razão para a existência dos números negativos é que tornou possível resolver todas as equações da forma: a + x = b para a incógnita x; nos números naturais apenas algumas destas equações eram solúveis.
Como os números naturais, os inteiros formam um conjunto infinito contável.
Pertencem ao conjunto dos números inteiros os números negativos, os números positivos e o zero. Fazendo uma comparação entre os números naturais e os inteiros percebemos que o conjunto dos naturais está contido no conjunto dos inteiros.
N = { 0,1,2,3,4,5,6, ... }
Z = { ... , -3,-2,-1,0,1,2,3,4, ... }
N C Z
O conjunto dos números inteiros é representado pela letra Z maiúscula. Os números positivos são representados com o sinal de (+) positivo na frente ou com sinal nenhum (+2 ou 2), já os números negativos são representados com o sinal de negativo (-) na sua frente (-2).
►Os números inteiros são encontrados com freqüência em nosso cotidiano, por exemplo:
♦ Exemplo 1:
Um termômetro em certa cidade que marcou 10°C acima de zero durante o dia, à noite e na manhã seguinte o termômetro passou a marcar 3°C abaixo de zero. Qual a relação dessas temperaturas com os números inteiros? Quando falamos acima de zero, estamos nos referindo aos números positivos e quando falamos dos números abaixo de zero estamos referindo aos números negativos.
N = { 0,1,2,3,4,5,6, ... }
Z = { ... , -3,-2,-1,0,1,2,3,4, ... }
N C Z
O conjunto dos números inteiros é representado pela letra Z maiúscula. Os números positivos são representados com o sinal de (+) positivo na frente ou com sinal nenhum (+2 ou 2), já os números negativos são representados com o sinal de negativo (-) na sua frente (-2).
►Os números inteiros são encontrados com freqüência em nosso cotidiano, por exemplo:
♦ Exemplo 1:
Um termômetro em certa cidade que marcou 10°C acima de zero durante o dia, à noite e na manhã seguinte o termômetro passou a marcar 3°C abaixo de zero. Qual a relação dessas temperaturas com os números inteiros? Quando falamos acima de zero, estamos nos referindo aos números positivos e quando falamos dos números abaixo de zero estamos referindo aos números negativos.
+10° C ------------- 10° C acima de zero
- 3° C --------------- 3° C abaixo de zero
- 3° C --------------- 3° C abaixo de zero
♦ Exemplo 2:
Vamos imaginar agora que uma pessoa tem R$500,00 depositados num banco e faça sucessivas retiradas:
• dos R$500,00 retira R$200,00 e fica com R$300,00
• dos R$300,00 retira R$200,00 e fica com R$100,00
• dos R$100,00 retira R$200,00 e fica devendo R$ 100,00 A última retirada fez com que a pessoa ficasse devendo dinheiro ao banco. Assim:
• dos R$300,00 retira R$200,00 e fica com R$100,00
• dos R$100,00 retira R$200,00 e fica devendo R$ 100,00 A última retirada fez com que a pessoa ficasse devendo dinheiro ao banco. Assim:
Dever R$100,00 significa ter R$100,00 menos que zero. Essa dívida pode ser representada por – R$100,00.
►Oposto de um número inteiro
O oposto de um número positivo é um número negativo simétrico. Por exemplo: o oposto de +2 é -2; o oposto de -3 é +3.
►O conjunto dos números inteiros possui alguns subconjuntos:
- Inteiros não – nulos
São os números inteiros, menos o zero.
Na sua representação devemos colocar * ao lado do Z.
Z* = {..., -3, -2, -1, 1, 2, 3,...}
- Inteiros não positivos
São os números negativos incluindo o zero.
Na sua representação deve ser colocado - ao lado do Z.
Z_ = {..., -3, -2, -1, 0}
- Inteiros não positivos e não – nulos São os números inteiros do conjunto do Z_ excluindo o zero.
Na sua representação devemos colocar o _ e o * ao lado do Z.
Z*_ = {..., -3, -2, -1}
- Inteiros não negativos
São os números positivos incluindo o zero.
Na sua representação devemos colocar o + ao lado do Z.
Z + = { 0,1 ,2 ,3, 4,...}
O Conjunto Z + é igual ao Conjunto dos N
- Inteiros não negativos e não - nulos
São os números do conjunto Z+, excluindo o zero.
Na sua representação devemos colocar o + e o * ao lado do Z.
Z* + = {1, 2, 3, 4,...} O Conjunto Z* + é igual ao Conjunto N*
CURIOSIDADES
| ||||||||||||||
Você sabia que a diferença de um número com o outro que obtemos escrevendo-o de trás para frente é igual a zero ou a um múltiplo de nove? Veja alguns exemplos:
22 - 22 = 0
51 - 15 = 36 (múltiplo de 9)
444 - 444 = 0
998 - 899 = 99 (múltiplo de 9)
1350 - 0531 = 819 (múltiplo de 9)
654321 - 123456 = 530865 (múltiplo de 9)
22 - 22 = 0
51 - 15 = 36 (múltiplo de 9)
444 - 444 = 0
998 - 899 = 99 (múltiplo de 9)
1350 - 0531 = 819 (múltiplo de 9)
654321 - 123456 = 530865 (múltiplo de 9)
DESAFIOS:
1 - DETERMINE O MENOR NÚMERO NATURAL CUJA:
- DIVISÃO POR 2 TEM RESTO 1;
- DIVISÃO POR 3 TEM RESTO 2;
- DIVISÃO POR 4 TEM RESTO 3;
- DIVISÃO POR 5 TEM RESTO 4;
- DIVISÃO POR 6 TEM RESTO 5;
- DIVISÃO POR 7 TEM RESTO 0.
Resposta: Suponhamos que estamos procurando o número X. Observe essas condições exigidas pelo problema:
X dividido por 2 dá resto 1.
X dividido por 3 dá resto 2.
e assim por diante até:
X dividido por 6 dá resto 5.
Então podemos notar que o resto dá sempre uma unidade a menos do que o divisor.
Isso significa que o número seguinte ao número X, ou seja, X+1, será divisível por 2,3,4,5 e 6.
Bom...já que X+1 é divisível por esses cinco números, então o número X+1 pode ser igual a 4x5x6=120.
Portanto, se X+1 é igual a 120, o número X que estamos procurando é 119, que também é divisível por 7.
2 - Um pequeno caminhão pode carregar 50 sacos de areia ou 400 tijolos. Se foram colocados no caminhão 32 sacos de areia, quantos tijolos pode ainda ele carregar?
Resposta: 1 saco de areia = 8 tijolos.
Se o caminhão pode carregar ainda 18 sacos então pode carregar 18 ´ 8 = 144 tijolos.
Fontes:
http://www.brasilescola.com/matematica/numeros-inteiros.htm
Referências Bibliográficas:
IMENES, Luiz Marcio; LELLIS, Marcelo. Matemática para todos. São Paulo: Ed. Scipione, 2002.
Referências Bibliográficas:
IMENES, Luiz Marcio; LELLIS, Marcelo. Matemática para todos. São Paulo: Ed. Scipione, 2002.
GIOVANNI, José Ruy & GIOVANNI, José Ruy. Pensar & descobrir. São Paulo: FTD, 2005.
Vídeos:
Assinar:
Postagens (Atom)












